Question

Find the radius of a circle with the equation:
x2 + y2 – 18x – 14y + 124 = 0

Answer 1

The radius of
`x^(2)+y^(2)-18\cdot x - 14\cdot y +124 = 0` is
`√(6)`.

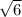Explanation:

The given expression must be converted into the standard form of a circle, which is described by:

`(x-h)^(2)+(y-k)^(2) = r^(2)`

Where:

`h`,
`k` - Location of center, dimensionless.

`r` - Radius, dimensionless.

The expression is modified algebraically as follows:

1)
`x^(2)+y^(2)-18\cdot x - 14\cdot y +124 = 0` Given

2)
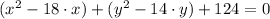`(x^(2)-18\cdot x)+(y^(2)-14\cdot y)+124 = 0` Commutative and associative properties.

3)
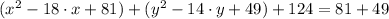`(x^(2)-18\cdot x+81)+(y^(2)-14\cdot y +49)+124 = 81+49` Commutative and associative properties/Compatibility with addition

4)
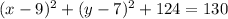`(x-9)^(2)+(y-7)^(2) + 124 = 130` Perfect square binomial/Definition of sum

5)
`(x-9)^(2)+(y-7)^(2) = 6` Compatibility with addition/Existence of additive inverse/Modulative property/Result

Given that
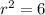`r^(2) = 6`, the radius of the circle is
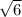`√(6)`.