Question

11.Avery and Bradly work at a large electronic manufacturer that produces DVD players. The defective rate on the assembly line has gone up 12% and the manager wants to know the probability that a skid of 50 DVD players will contain at least 3 defective units. Help Avery use the binomial distribution P(x)=n Cx p^x q^n-x to answer this question

Answer 1

The probability that a skid of 50 DVD players will contain at least 3 defective units is 0.9487.

Explanation:

We are given that Avery and Bradly work at a large electronics manufacturer that produces DVD players. The defective rate on the assembly line has gone up 12% and a skid of 50 DVD players has been selected by the manager.

Let X = Number of defective units of DVD players

The above situation can be represented through the binomial distribution;

`P(X = r) = \binom{n}{r}* p^(2) * (1-p)^(n-r); x= 0,1,2,3,....`

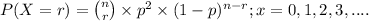
where, n = number of samples (trials) taken = 50 DVD players

r = number of success = at least 3 defective units

p = probability of success which in our question is the probability

of defective rate, i.e; p = 12%

So, X ~ Binom(n = 50, p = 0.12)

Now, the probability that a skid of 50 DVD players will contain at least 3 defective units is given by = P(X
`\geq` 3)

P(X
`\geq` 3) = 1 - P(X = 0) - P(X = 1) - P(X = 2)

=
`1 - [ \binom{50}{0}* 0.12^(0) * (1-0.12)^(50-0)]-[ \binom{50}{1}* 0.12^(1) * (1-0.12)^(50-1)]-[ \binom{50}{2}* 0.12^(2) * (1-0.12)^(50-2)]`

=
`1 - [ 1 * 1 * 0.88^(50)]-[50 * 0.12^(1) * 0.88^(49)]-[ 1225 * 0.12^(2) * 0.88^(48)]`

= 0.9487

Hence, the probability that a skid of 50 DVD players will contain at least 3 defective units is 0.9487.