Question

What is the purpose of multiplying by the conjugate of a complex denominator when finding the quotient of complex numbers?

Answer 1

Answer: To have a real number in the denominator

Explanation:

Ok, a quotient between two complex numbers can be written as:

`(A + Bi)/(C+Di)`

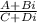
Now, when we do these types of divisions, we multiply and divide by the same number (so in essence we are multiplying by one) that is the conjugate of the denominator.

Remember that for a complex number:

Z = A + Bi

the conjugate is = A - Bi.

Then, wen we multiply the denominator by it's conjugate, we have:

(C + Di)(C - Di) = C^2 + D*C*i - D*C*i + (D*i)*(-D*i) = C^2 + D^2

So now we have a real number in the denominator (the imaginary part of this number is equal to zero)

So the answer to the question is:

"To have a real number in the denominator"