Question

An investigator predicts that dog owners in the country spend more time walking their dogs than do dog owners in the city. The investigator gets a sample of 21 country owners and 23 city owners. The mean number of hours per week that city owners spend walking their dogs is 10.0. The standard deviation of hours spent walking the dog by city owners is 3.0. The mean number of hours country owners spent walking theirs dogs per week was 15.0. The standard deviation of the number of hours spent walking the dog by owners in the country was 4.0. Do dog owners in the country spend more time walking their dogs than do dog owners in the city?

Answer 1

Yes dog owners in the country spend more time walking their dogs than do dog owners in the city

Explanation:

From the question we are told that

The sample size from country is
`n_1 = 21`

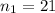
The sample size from city is
`n_2 = 23`

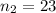
The sample mean for country is
`\= x_1 =  15`

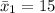
The Sample mean for city is
`\= x_2 =  10`

The standard deviation for country is
`\sigma _1 =  4`

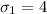
The standard deviation for city is
`\sigma _2 =  3`

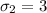
Let the level of significance is
`\alpha = 0.05`

The null hypothesis is
`H_o : \mu_1 = \mu_2`

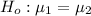
The alternative hypothesis is
`H_a : \mu_1 > \mu_2`

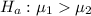
The pooled standard deviation is mathematically represented as

`s =  \sqrt{ (s_1 ^2  *  (n_1 - 1 ) + s_2 ^2 *  (n_2 - 1 ))/( df) }`

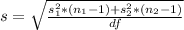
Here df is the degree of freedom which is mathematically represented as

`df =  n_1 + n_2  - 2`

`df =  21 + 23 -2`

`df =  42`

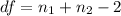
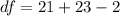
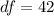
So

`s =  \sqrt{ (4 ^2  *  (15.0 - 1 ) + 3 ^2 *  (10 - 1 ))/( 42) }`

`s =  3.5`

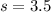
Generally the test statistics is mathematically represented

`t =  \frac{\= x_1 - \= x_2 }{ s *  \sqrt{(1)/(n_1) +(1)/(n_2)  } }`

`t =  \frac{ 15 -10 }{ 3.5 * \sqrt{(1)/( 21 ) + (1)/(23) } }`

`t =  4.733`

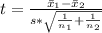
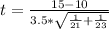
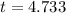
Generally the p-value is obtained from the student t-distribution table table , the value is

`P(T >   4.733)=  t_(4.733,  42 ) = 0.000013`

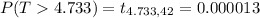
From the calculation we see that

`p-value  < \alpha`

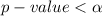
So we reject the null hypothesis

Hence we can conclude that there is sufficient evidence to support the claim that dog owners in the country spend more time walking their dogs than do dog owners in the city