Answer: see proof below
Explanation:
Use the Sum/Difference Identity: tan (A + B) = (tanA + tanB)/(*1 - tanA · tanB)
Scratchwork:
tan (50) = tan (40 + 10)
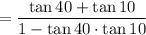
tan 50 (1 - tan 40 · tan 10) = tan 40 + tan 10
tan 50 - tan 50 · tan 40 · tan 10 = tan 40 + tan 10
tan 50 = tan 40 + tan 10 + tan 50 · tan 40 · tan 10
Use the Reciprocal Identity: cot A = 1/ tan --> cot A · tan A = 1
Proof LHS → RHS
LHS: tan 50 - tan 40
Substitute tan 50: tan 40 + tan 10 + (tan 50 · tan 40) · tan 10 - tan 40
Simplify: tan 10 + (tan 50 · tan 40) · tan 10
Reciprocal Identity: tan 10 + tan 10
Simplify: 2 tan 10
LHS = RHS: 2 tan 10 = 2 tan 10