The correct answer is D. None of the above
Polynomials in standard form typically have the terms arranged in descending order of degree and do not skip any degrees.
The standard form of a polynomial is usually written as:
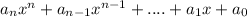
where
 is the coefficient of the highest degree term,
is the coefficient of the highest degree term,
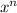 .
.
Now, let's check the given polynomials:
A. -1: This is not a polynomial; it's a constant term.
B.
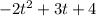 : This is not in standard form as the terms are not arranged in descending order of degree.
: This is not in standard form as the terms are not arranged in descending order of degree.
C. 4t−7: This is in standard form as it's a linear polynomial (degree 1), and the terms are in the correct order.
D. None of the above: This would be the correct answer since only option C is in standard form.
So, the correct answer is D. None of the above