Question

A Pipe Filled with Helium A certain organ pipe, open at both ends, produces a fundamental frequency of 293 Hz in air Now consider a pipe that is stopped (i.e., closed at one end) but still has a fundamental frequency of 293 Hz in air. How does your answer to Part A, fHe, change

Answer 1

Complete question:

A certain organ pipe, open at both ends, produces a fundamental frequency of 293 Hz in air. If the pipe is filled with helium at the same temperature, what fundamental frequency fHe will it produce? Take the molar mass of air to be 28.97 g/mol and the molar mass of helium to be 4.00 g/mol. Now consider a pipe that is stopped (i.e., closed at one end) but still has a fundamental frequency of 293 Hz in air. How does your answer to first question, fHe, change?

Answer:

The fundamental frequency that helium produced is 788.6 Hz.

Since the fundamental frequency of air in closed pipe is still the same value as open pipe, the fundamental frequency of helium will not change.

Step-by-step explanation:

The speed of sound in pipe when filled with air is given by;

`v = \sqrt{(\gamma RT)/(M) }`

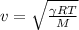
Where;

γ = 1.4

R = 8.31 J/mol.K

M = 0.02897 kg/mol

T = 20°C = 293 K

`v_(air) = \sqrt{(1.4* 8.31*293)/(0.02897) } = 343 \ m/s`

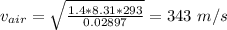
The speed of sound in pipe when filled with helium is given by

`v_(He) = \sqrt{(1.4* 8.31*293)/(0.004) } =923.14 \ m/s`

Now, determine the fundamental frequency Helium will it produce

v = fλ

`\frac{V_(air)}{F_o{air}} = \frac{V_(He)}{F_o{He}}\\\\F_o{He} = \frac{F_o{air}*V_(He)}{V_(air)} \\\\F_o{He} = ((293)*(923.14))/(343)\\\\F_o{He} = 788.6 \ Hz`

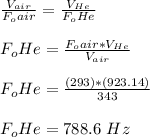
Since the fundamental frequency of air in closed pipe is still the same value as open pipe, the fundamental frequency of helium will not change.