Question

89, 74, 100, 86, 74, 67, 86, 72, 60, 93, 83, 86 what is the median?

Answer 1

`\boxed{ \bold{ \huge{ \boxed{ \sf{84.5}}}}}`

Explanation:

Given data :

89 , 74 , 100 , 86 , 74 , 67 , 86 , 72 , 60 , 93 , 83 , 86

Arranging the data in ascending order, we have,

60 , 67 , 72 , 74 , 74 ,83 , 86 , 86 , 86 , 89 , 93 , 100

Here, n ( total no.of observation ) = 12

Now, finding the position of media :

`\boxed{ \sf{position \: of \: median = ( (n + 1)/(2) ) ^(th) \: item}}`

⇒
`\sf{ ((12 + 1)/(2) ) ^(th) item}`

⇒
`\sf{( (13)/(2) ) ^(th) item}`

⇒
`\sf{ {6.5}^(th) item}`

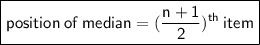
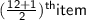
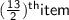
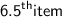
6.5 th item is the average of 6 th and 7 th items.

Again,

`\sf{median = \frac{ {6}^(th \: item) + {7}^(th) item}{2} }`

⇒
`\sf{ (83 + 86)/(2) }`

⇒
`\sf{ (169)/(2) }`

⇒
`\sf{84.5}`

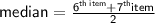
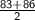
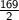
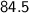
Hope I helped!

Best regards!!