Question

Find the coordinates of the other endpoint of the​ segment, given its midpoint and one endpoint.​ (Hint: Let​ (x,y) be the unknown endpoint. Apply the midpoint​ formula, and solve the two equations for x and​ y.) midpoint ​(8​,5​), endpoint ​(​10,​8)

Answer 1

Explanation:

Hey, there!!

Here, one point is A(10,8) and P(8,5) is the midpoint.

Let B(x,y) be the another end point.

Now,

Using midpoint formulae,

`p(x.y) = (x1 + x2)/(2) . (y1 + y2)/(2)`

`p(8.5) = ( (10 + x)/(2) . (8 + y)/(2) )`

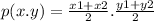
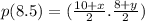
Since they are equal,equating with their corresponding elements we get,

`8 = (10 + x)/(2)`

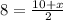
or, 16 = 10 + x

or, x=16-10

Therefore, x = 6

Now,

`5 = (8 + y)/(2)`

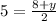
or, 10 = 8 + y

or, y = 2

Therefore, The coordinates of another point are B(6,2)

Hope it helps .....