Answer:
see explanation
Explanation:
Using the sum/ difference → product formula
cos x - cos y = - 2sin(
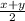 )sin (
)sin (
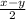 )
)
sin x - sin y = 2cos (
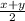 )sin (
)sin (
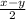 )
)
Given
(cosA - cosB)² + (sinA - sinB )²
= [ - 2sin(
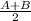 )sin(
)sin(
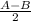 ) ]² + [ 2cos(
) ]² + [ 2cos(
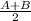 )sin(
)sin(
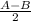 ) ]²
) ]²
= 4sin² (
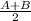 )sin² (
)sin² (
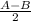 ) + 4cos² (
) + 4cos² (
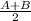 )sin² (
)sin² (
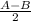 )
)
= 4sin² (
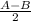 )[ sin² (
)[ sin² (
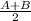 ) + cos² (
) + cos² (
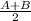 ) ← sin²x + cos²x = 1
) ← sin²x + cos²x = 1
= 4sin² (
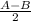 ) × 1
) × 1
= 4sin² (
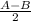 ) = right side ⇒ proven
) = right side ⇒ proven