Question

If a+b+c=2 , ab+bc+ac= -1 and abc = -2 , then find the value of a^3 + b^3 + c^3

Answer 1

Answer: 8

Explanation:

EQ1: a + b + c = 2 --> b + c = 2 - a

EQ2: ab + bc + ac = -1 --> b + c = (-1 - bc)/a

EQ3: abc = -2 --> bc = -2/a

Set EQ1 = EQ2 and substitute bc using EQ3 to solve for "a":

`2-a=(-1-bc)/(a)\\\\\\\text{Clear the denominator:}\\a(2-a)=-1-bc\\\\\text{Substitute bc:}\\a(2-a)=-1-(-2)/(a)\\\\\\\text{Clear the denominator:}\\a^2(2-a)=-a+2\\\\\\\text{Simplify and set equal to 0:}\\2a^2-a^3=-a+2\\0=a^3-2a^2-a+2\\\\\text{Factor:}\\0=a^2(a-2)-1(a-2)\\0=(a^2-1)(a-2)\\\\\text{Solve for a:}\\a^2-1=0\qquad a-2=0\\a=\pm1}\qquad \qquad a=2`

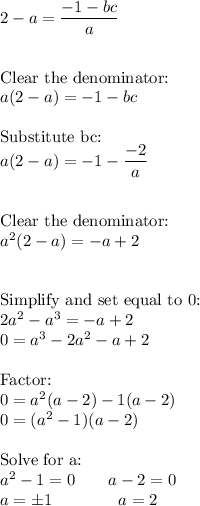
Consider the solution a = 2 and plug it into EQ1 to solve for "b"

b + c = 2 - 2

b + c = 0

b = -c

Plug in a = 2, b = -c, and c = c into a³ + b³ + c³

2³ + (-c)³ + c³

= 8 - c³ + c³

= 8