Question

Need the answer ASAP

Answer 1

Approximately 201 squared inches.

Explanation:

So, the composite figure is made up of a square and a semi-circle. The square has side lengths of 12 and the semi-circle has a radius of 6.

The total area of the figure would be the area of the square plus the area of the semi-circle. Thus, find the area of each individual figure.

Square:

The area of a square is given by:

`A=l^2`

Where l is the side length.

Substitute 12 for l:

`A=(12)^2\\A=144\text{ in}^2`

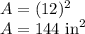
So the square is 144 square inches.

Semi-circle:

The area of a semi-circle is given by:

`A=(1)/(2)\pi r^2`

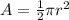
Substitute 6 for r and 3.14 for π:

`A=(1)/(2)(3.14)(6)^2\\ A=56.52`

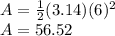
Therefore, the total area is:

`TA=144+56.52\\TA=200.52\text{ in}^2\approx201\text{ in}^2`