Question

The area of a rectangle is 56 cm. the length is 2 less than x and the width is 5 less than twice of x. solve for x

Answer 1

`x=(9+√(449))/(4)`

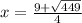
Explanation:

The area of a rectangle is:

`A=l\cdot w`

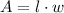
First let's write both the length and the width in terms of x:

`l=x-2`

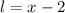
How we obtained the answer:

The question states the length is "2 less than x". In this case, "less" is a keyword that represents subtraction. Therefore, "2 less than x" is "x-2".

`w=2x-5`

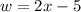
How we obtained the answer:

The question states the width is "5 less than twice of x". First, start by figuring out what "twice of x" is. The keyword is "twice" which represents multiplication. Therefore, "twice of x" can be written as "2x". Then, using the same keyword from before ("less"), "5 less than..." represents "2x-5".

Given:

Area = 56 cm

`l=x-2`

`w=2x-5`

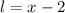
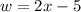
Find:

x

`A=l\cdot w`

`56=(x-2)(2x-5)`

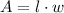
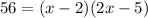
FOIL (Firsts, outsides, insides, lasts):

`56=2x^2-4x-5x+10\\56=2x^2-9x+10`

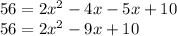
Subtract 10 from both sides:

`46=2x^2-9x`

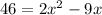
Subtract 46 from both sides (forms a quadratic equation):

`0=2x^2-9x-46`

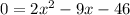
Use the quadratic formula:

`{x = \frac{{ - b \pm \sqrt {b^2 - 4ac} }}{{2a}}}` where
`0=ax^2+bx+c`

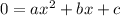
Therefore:

`x=(9\pm√(81-4(2)(-46)))/(2(2))\\x=(9\pm√(81+368))/(4)\\\\x=(9\pm√(449))/(4)`

The answer is:

`x=(9+√(449))/(4)`

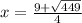
This is because if we used subtraction, we would get a negative value, and we cannot have a negative length/width.