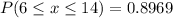Answer:
a
mean
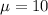 variance
variance
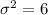
b
The binomial random variable x fall into this interval ranges from
- 5 to 5
c
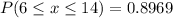
Explanation:
From the question we are told that
The sample size is

The percentage that look for gas stations and food outlets that are close to or visible from the highway is
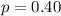
Generally the mean is mathematically represented as

=>

=>
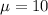
The variance is mathematically represented as
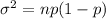
=>
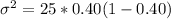
=>
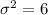
The standard deviation is mathematically evaluated as
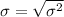

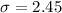
The interval is evaluated as
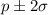
=>
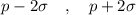
=>
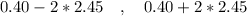
=>
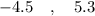
The binomial random variable x fall into this interval ranges from
- 5 to 5
Generally
![P(6 \le x \le 14) = P(( x - \mu )/(\sigma ) \le \frac{14 - 10}{{2.45}} ]-P[ ( x - \mu )/(\sigma ) \le (6 - 10)/(2.45 ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/nyu6r7fn7fy70jebkvyxj411t7k3ove2qt.png)
![P(6 \le x \le 14) = P(Z \le 1.63 ]-P[ Z \le -1.63 ]](https://img.qammunity.org/2021/formulas/mathematics/college/cq1cyy2j01nv5e8y5kws48hsakverlz29x.png)
![P(6 \le x \le 14) = [1- P(Z > 1.63 ]] -[1- P[ Z > -1.63 ]]](https://img.qammunity.org/2021/formulas/mathematics/college/vro1uwcyjcz1cjjaybhneocx1ws3hykxuc.png)
From the z-table
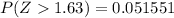
And
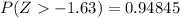
=>
![P(6 \le x \le 14) = [1-0.051551] -[1-0.94845]](https://img.qammunity.org/2021/formulas/mathematics/college/gzg2b3qav9o1vmsju5lodc6d641dhewoes.png)
=>