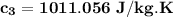Question

A laboratory technician drops a 0.0850 kg sample of unknown solid material, at a temperature of 100 oC, into a calorimeter. The calorimeter can, initially at 19.0 oC, is made of 0.150 kg of copper and contains 0.20 kg of water. The final temperature of the calorimeter can, and contents is 26.1 oC. Compute the specific heat of the sample.

Answer 1

The specific heat of the sample
`\mathbf{c_3 = 1011.056 \ J/kg.K}`

Step-by-step explanation:

Given that:

mass of an unknown sample
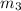`m_3` = 0.0850

temperature of the unknown sample
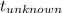`t_(unknown)` = 100° C

initial temperature of the calorimeter can = 19° C

mass of copper
`m_1` = 0.150 kg

mass of water
`m_2`= 0.20 kg

the final temperature of the calorimeter can = 26.1° C

The objective is to compute the specific heat of the sample.

By applying the principle of conservation of energy

`Q = mc \Delta T`

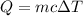
where;

`Q_1 +Q_2 +Q_3 = 0`

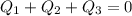
i.e

`m_1 c_1 \Delta T_1 +m_2 c_2 \Delta T_2+m_3 c_3 \Delta T_3 =0`

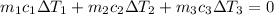
the specific heat capacities of water and copper are 4.18 × 10³ J/kg.K and 0.39 × 10³ J/kg.K respectively

the specific heat of the sample
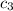`c_3` can be computed by making
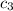`c_3` the subject of the above formula:

i.e

`c_3 = (m_1 c_1 \Delta T_1 +m_2 c_2 \Delta T_2)/(m_3 c_3 \Delta T_3)`

`c_3 = ( 0.150 * 0.39 * 10^3 * (26.1 -19) + 0.20 * 4.18 * 10^3 * (26.1 -19) )/(0.0850 * (100-26.1 ))`

`c_3 = ( 0.150 * 0.39 * 10^3 * (7.1) + 0.20 * 4.18 * 10^3 * (7.1) )/(0.0850 * (73.9))`

`c_3 = (415.35 + 5935.6 )/(6.2815)`

`c_3 = (415.35 + 5935.6 )/(6.2815)`

`c_3 = (6350.95)/(6.2815)`

`\mathbf{c_3 = 1011.056 \ J/kg.K}`

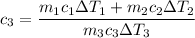
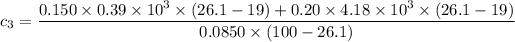
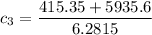
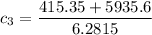
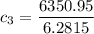
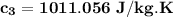
The specific heat of the sample
`\mathbf{c_3 = 1011.056 \ J/kg.K}`