Answer:
The rate of the jet in still air is 852 miles per hour. The rate of the wind is 85 miles per hour.
Explanation:
Let suppose that jet travels uniformly, that is, at constant speed, the expressions for its travels against the wind and with the wind are, respectively:
Against the wind

With the wind
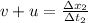
Where:
 - Speed of the jet in still air, measured in miles per hour.
- Speed of the jet in still air, measured in miles per hour.
 - Speed of wind, measured in miles per hour.
- Speed of wind, measured in miles per hour.
 ,
,
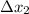 - Distances travelled by jet against the wind and with the wind, measured in miles.
- Distances travelled by jet against the wind and with the wind, measured in miles.
 ,
,
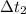 - Times against the wind and with the wind, measured in hours.
- Times against the wind and with the wind, measured in hours.
By adding both expressions:
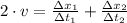
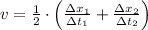
Given that
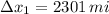 ,
,
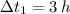 ,
,
 and
and
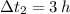 , the speed of the jet is:
, the speed of the jet is:
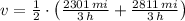
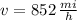
The rate of the jet in still air is 852 miles per hour.
Lastly, the rate of the wind is:
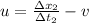
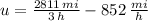
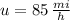
The rate of the wind is 85 miles per hour.