Answer:
A kite
Explanation:
The coordinates of the vertices of the quadrilateral are;
A(2, 3), B(4, 6), C(8, 9), and D(5, 5), therefore, the length of the sides of the quadrilateral can be found using the following formula;
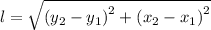
(x₁, y₁) and (x₂, y₂) are the coordinates of the two endpoints on the side
For side AB, we have;
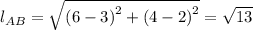
The slope = 1.5
For side BC, we have;
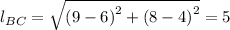
The slope = 3/4
For side CD, we have;
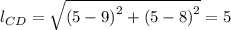
The slope = 4/3
For side DA, we have;
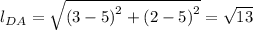
The slope = 2/3
Angle ADC = Actan (2/3 - 4/3)/(1 + 2/3*4/3) = -19.44 = 180-19.44 = 160.55°
Angle ABC = Actan (0.75 - 1.5)/(1 + 0.75*1.5) = -19.44 = 180-19.44 = 160.55°
Therefore, given that the quadrilateral has two pairs of equal adjacent sides and the angles are equal at the meeting point of the two squares, it is best described as a kite.