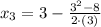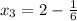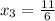Answer:
The first and second iteration of Newton's Method are 3 and
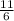 .
.
Explanation:
The Newton's Method is a multi-step numerical method for continuous diffentiable function of the form
 based on the following formula:
based on the following formula:
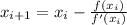
Where:
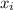 - i-th Approximation, dimensionless.
- i-th Approximation, dimensionless.
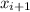 - (i+1)-th Approximation, dimensionless.
- (i+1)-th Approximation, dimensionless.
 - Function evaluated at i-th Approximation, dimensionless.
- Function evaluated at i-th Approximation, dimensionless.
 - First derivative evaluated at (i+1)-th Approximation, dimensionless.
- First derivative evaluated at (i+1)-th Approximation, dimensionless.
Let be
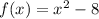 and
and
 , the resultant expression is:
, the resultant expression is:
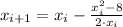
First iteration: (
 )
)

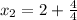
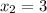
Second iteration: (
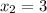 )
)