Answer:
The sum of all the even integers between 99 and 301 is 20200
Explanation:
For the sum of all the even integers between 99 and 301, this can be calculated using the formula for Sum of n terms in an Arithmetic Progression (AP)
Sum of n terms in an AP
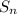 =
=
![(n )/(2)[ 2a + (n - 1)d]](https://img.qammunity.org/2021/formulas/mathematics/high-school/7pjd3r3phzpd5oztmrf2vdha550bks65xw.png)
Where
 is the number of terms
is the number of terms
 is the first term
is the first term
and
 is the common difference
is the common difference
The AP for the sum of all the even integers between 99 and 301 will look like
100 + 102 + 104 + ... + 300
 = 100
= 100
 can be calculated by taking the difference of the first two terms or any two consecutive terms of the AP
can be calculated by taking the difference of the first two terms or any two consecutive terms of the AP
Hence,
 = 102 - 100 = 2
= 102 - 100 = 2
 can be determined from the formula used to calculate the Last term of an AP
can be determined from the formula used to calculate the Last term of an AP
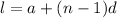
Where
 is the last term
is the last term
In the AP, the last term,
 = 300
= 300
Then
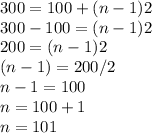
Hence, there are 101 terms in the AP
Now, to determine the sum
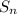 =
=
![(n )/(2)[ 2a + (n - 1)d]](https://img.qammunity.org/2021/formulas/mathematics/high-school/7pjd3r3phzpd5oztmrf2vdha550bks65xw.png)
![S_(n) =(101)/(2)[ 2(100) + (101 - 1)2]\\ S_(n)=(101)/(2)[ 200 + (100)2]\\ S_(n)=(101)/(2)[ 200 + 200]\\S_(n)=(101)/(2)[ 400]\\S_(n) = 20200](https://img.qammunity.org/2021/formulas/mathematics/high-school/5glf5i23uizfyvcz25ind5jg1904mwmk5y.png)
Hence, the sum of all the even integers between 99 and 301 is 20200