Question

The sum of squares of three consecutive numbers is 77 find the numbers​

Answer 1

4,5,6 are the three consecutive numbers. 16, 25 and 36 are their squares.

Explanation:

Let the three consecutive numbers be x, (x+1), (x+2)

Now, the squares of these three numbers are
`x^(2) ,(x+1)^(2) ,(x+2)^(2)`

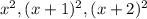
Sum = 77

∴by the problem ,

`x^(2) +(x+1)^(2)+(x+2)^(2) = 77\\x^(2) +(x^(2) +2x+1)+(x^(2)+4x +4) = 77\\x^(2) +x^(2) +2x+1+x^(2) +4x +4 = 77\\3x^(2) +6x+5 = 77\\3x^(2) +6x = 77-5\\3x^(2) + 6x = 72\\3x^(2) +6x-72= 0\\`

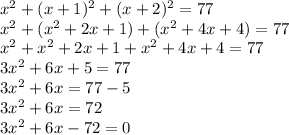
{Taking 3 common }

`x^(2) +2x- 24 = 0\\`

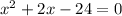
{By factorization}

`x^(2) +2x- 24 =0\\ x^(2) +6x-4x-24=0\\x(x+6)-4(x+6)=0\\(x+6)(x-4)=0\\`

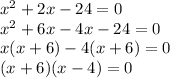
Therfore,

`x= -6,4\\`

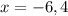
X can't be negetive

∴
`x =4\\x+1=5\\x+2=6`

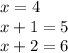
The squares of the three consecutive numbers are 16, 25, 36

The three consecutive numbers whose sum is 77 are 4, 5, 6