Answer:
135
Explanation:
From the given information:
The total number of handshakes can be represented by the combination of 18 combination 2, which can be mathematically expressed as:
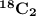 .
.
where;
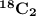 is the number of ways two people can shake themselves from a total of 28 people without much regard about the order of arrangement of the handshakes.
is the number of ways two people can shake themselves from a total of 28 people without much regard about the order of arrangement of the handshakes.


= 153
From these 6 companies, the possibility that there will be handshakes from within the company is
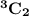
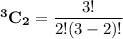
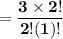
= 3
However, number of companies = 6
∴ the number of handshakes within companies = 3 × 6 = 18
But we are being told that :
If the representatives did not shake hands with people from their own company, how many handshakes took place
Therefore, the number of handshakes that took place in regard to the given criteria = 153 - 18
= 135