Question

Find the sum of the convergent series by using a well-known function. (Round your answer to four decimal places.) [infinity] (−1)n + 1 1 7nn n = 1

Answer 1

Here is the full question:

Find the sum of the convergent series by using a well-known function. (Round your answer to four decimal places.) Σ_(n=1)^∞ (-1)^n+1 1/7^n n

Explanation:

Σ_(n=1)^∞ (-1)^n+1 1/7^n n

We will use the function In (1 + x)

We will now give a power series expansion of the function while it is centered at x=0

This will give us In (1 + x) = Σ_(n=1)^∞
`(-1)^(n+1)`
`(x^(n) )/(n)`

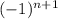
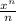
Note that x= 1/7

Now let us equate the two equations

Σ_(n=1)^∞
`(-1)^(n+1)`
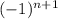
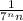`(1)/(7^(n)n )` = ㏑(1 + x)|
`_{x = (1)/(7) }` = ㏑
`(8)/(7)`

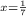Sum of the series will give ㏑
`(8)/(7)`