Question

You want to buy a special handcrafted square box. Since each box is uniquely handcrafted and you did not bring you ruler, you are not sure of the exact dimensions. Let X be the length of one of the sides, and assume that X is uniformly distributed between 15 and 18 inches. a) What is the expected volume of the box that you buy

Answer 1

`Volume = 4492.125\ unit^3`

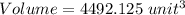
Explanation:

Given

Uniform Distribution X

X: 15 to 18

Required

Determine the expected volume

Since, X is uniformly distributed; We have to first determine the expected value of X as follows;

`Mean(X) = (b + a)/(2)`

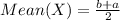
Where b = 18 and a = 15

`Mean(X) = (18 + 15)/(2)`

`Mean(X) = (33)/(2)`

`Mean(X) = 16.5`

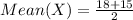
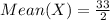
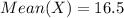
Since the box is a square box, the volume is as follows;

`Volume = 16.5 * 16.5 * 16.5`

`Volume = 4492.125\ unit^3`

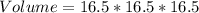
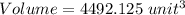
Hence, the expected volume is 4492.125 unit³