Question

Construct a​ 90% confidence​ interval, using the inequality . To test the effectiveness of a new drug that is reported to increase the number of hours of sleep patients get during the​ night, researchers randomly select 13 patients and record the number of hours of sleep each gets with and without the new drug.

Answer 1

The 90% confidence​ interval is (-1.987, -1.320).

Explanation:

The data provided is:

Sleep without Sleep using

the drug the drug d=without-with

2.5 4.3 -1.8

2.7 4.2 -1.5

3.8 5.0 -1.2

3.8 6.2 -2.4

1.8 2.5 -0.7

4.7 7.1 -2.4

4.8 7.1 -2.3

2.7 3.3 -0.6

1.8 3.5 -1.7

2.2 4.3 -2.1

3.6 4.3 -0.7

5.3 7.0 -1.7

5.2 7.6 -2.4

Compute the sample mean and sample standard deviation:

`\bar d=(1)/(n)\sum d=(1)/(13)* [(-1.8)+(-1.5)+(-1.2)+...+(-2.4)]=-1.654\\\\S_(d)=\sqrt{(1)/(n-1)\sum [d-\bar d]^(2)}=0.6753`

The degrees of freedom of the test is:

df = n - 1 = 13 - 1 = 12

Compute the critical value of t for 90% confidence​ level and 12 degrees of freedom as follows:

`t_(\alpha/2, (n-1))=t_(0.10/2, 12)=1.782`

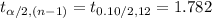
Compute the 90% confidence​ interval as follows:

`\bar d-t_(\alpha/2, (n-1))\cdot(S_(d))/(√(n))<\mu_(d)<\bar d+t_(\alpha/2, (n-1))\cdot(S_(d))/(√(n))`

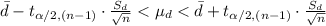
`-1.645-[1.782\cdot(0.6753)/(√(13))]<\mu_(d)<-1.645+[1.782\cdot(0.6753)/(√(13))]\\\\-1.645-0.334<\mu_(d)<-1.654+0.334\\\\-1.988<\mu_(d)<-1.320`

Thus, the 90% confidence​ interval is (-1.987, -1.320).