Question

Find the domain for the rational function f of x equals quantity x plus 1 end quantity divided by quantity x minus 2 end quantity.

(−[infinity], 2) (2, [infinity])

(−[infinity], −2) (−2, [infinity])

(−[infinity], 1) (1, [infinity])

(−[infinity], −1) (−1, [infinity])

Answer 1

`(- \infty, 2), (2, \infty)`

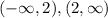
Explanation:

Given the function:

`f(x) = (x+1)/(x-2)`

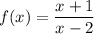
To find:

Domain of the function.

Solution:

First of all, let us learn about definition of domain of a function.

Domain of a function is the valid input values that can be provided to the function for which output is defined.

OR

Domain of a function
`f(x)` are the values of
`x` for which the output
`f(x)` is a valid value.

i.e. The function does not tend to
`\infty` or does not have
`\frac{0}0` form.

So, we will check for the values of
`x` for which
`f(x)` is not defined.

For value to tend to
`\infty`, denominator will be 0.

`x-2\\eq 0 \\\Rightarrow x \\eq 2`

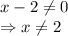
So, the domain can not have x = 2

Any other value of x does not have any undefined value for the function
`f(x)`.

Hence, the answer is:

`\bold{(- \infty, 2), (2, \infty)}` [2 is not included in the domain].