Answer:
E. -2, 4
Explanation:
If the zeroes of a function are given as
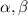 , then the function can be written as:
, then the function can be written as:
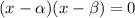
Here, we are given that zeros of
 are x=-1 and x=2.
are x=-1 and x=2.
As per above, we can write the function
 as:
as:
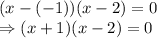
So,
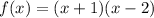
To find:
Zeroes of
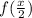 .
.
Solution:
We have found that
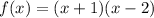
Replacing
 with
with
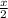 :
:
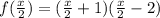
Now, Let us put it equal to 0 to find the zeroes.
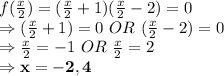
So, the zeroes are -2, 4.