Answer:
E
Explanation:
So we already know that:

So, go through each of the choices and see which ones are correct.
I)
We have:

This is the same as saying:

And since we already know the values:
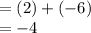
So, the limit does indeed exist.
II)
We have:
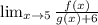
This is the same as:
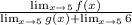
The bottom right one is just 6. Simplify:
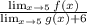
Substitute the values we know:
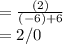
This is a value over zero. Unlike the indeterminate form 0/0, this limit does not exist.
III)
We have:
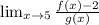
Again, this is the same as:
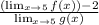
Substitute in the values we know:

The limit does exist and it is 0.
So, the limits of only I and III exist.
The correct answer is E.