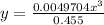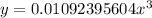Answer:
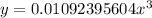
Explanation:
Given:
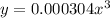
Where y is in pounds and x is in inches
Required
Represent y in kilogram and x in centimetre
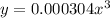
The expression can be rewritten as
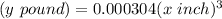
------------------------------------------------------------------------------------------------
If
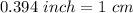
Divide both by 0.394
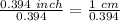
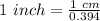
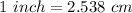 (Approximated)
(Approximated)
Multiply both sides by x
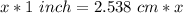

------------------------------------------------------------------------------------------------
If

Divide both by 2.20
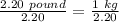
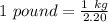
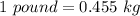 (Approximated)
(Approximated)
Multiply both sides by y

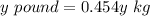
------------------------------------------------------------------------------------------------
Substitute 0.455y kg for y pound and 2.538x cm for x inch in
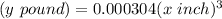

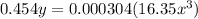 Approximated
Approximated
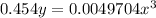
Divide both sides by 0.455