Question

The internal energy of 10 moles of helium (a monatomic gas) is 15 kJ. What is the rms speed of the molecules? (The molar mass of helium is 4.00 g/mole.)

Answer 1

`v_(rms)=866.32m/s`

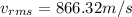
Step-by-step explanation:

Hello,

In this case, since the rms speed of the molecules is computed by:

`v_(rms)=\sqrt{(3RT)/(M) }`

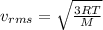
Whereas the absolute temperature is computed from the internal energy (by using the Cp of helium (3.1156 J/g*K) as shown below:

`U=nCvT\\\\T=(U)/(nCv)=(15kJ*(1000J)/(1kJ) )/(10mol*(4.00g)/(1mol) *3.1156(J)/(g*K) ) \\\\T=120.36K`

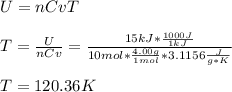
Thereby, the rms speed results:

`v_(rms)=\sqrt{(3*8.314(kg*m^2)/(s^2*mol*K)*120.36K)/(4.00(g)/(mol)*(1kg)/(1000) ) } \\\\v_(rms)=866.32m/s`

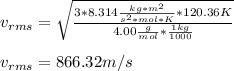
Regards.