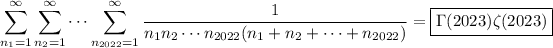Question

`\displaystyle \rm \sum_{ n_( 1) = 1}^ \infty \displaystyle \rm \sum_{ n_(2) = 1}^ \infty \dots \displaystyle \rm \sum_{ n_(2022) = 1}^ \infty (1)/(n_(1) n_2 \dots n_(2022)(n_(1) + n_2 + \dots + n_(2022)))`​

Answer 1

As a simpler example, consider the iterated sum with only 2 indices,

`\displaystyle \sum_(n_1=1)^\infty \sum_(n_2=1)^\infty \frac1{n_1n_2(n_1+n_2)}`

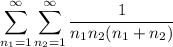
(The case with just one index is pretty simple, as it reduces to ζ(2) = π²/6.)

Let

`\displaystyle f(x) = \sum_(n_1=1)^\infty \sum_(n_2=1)^\infty (x^(n_1+n_2))/(n_1n_2(n_1+n_2))`

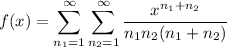
Differentiating and multiplying by x, we get

`\displaystyle x f'(x) = \sum_(n_1=1)^\infty \sum_(n_2=1)^\infty (x^(n_1+n_2))/(n_1n_2) \\\\ = \left(\sum_(n_1=1)^\infty(x^(n_1))/(n_1)\right) \left(\sum_(n_2=1)^\infty (x^(n_2))/(n_2)\right) \\\\ = (-\ln(1-x))^2 = \ln^2(1-x)`

`\implies f'(x) = \frac{\ln^2(1-x)}x`

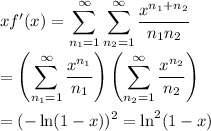
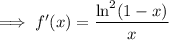
By the fundamental theorem of calculus (observing that letting x = 0 in the sum makes it vanish), we have

`f(x) = \displaystyle \int_0^x \frac{\ln^2(1-t)}t \, dt`

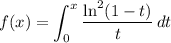
If we let x approach 1 from below, f(x) will converge to the double sum and

`\displaystyle \sum_(n_1=1)^\infty \sum_(n_2=1)^\infty \frac1{n_1n_2(n_1+n_2)} = \int_0^1 \frac{\ln^2(1-x)}x \, dx`

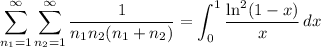
In the integral, substitute
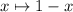`x\mapsto1-x`, use the power series expansion for 1/(1 - x), and integrate by parts twice.

`\displaystyle \int_0^1 \frac{\ln^2(1-x)}x \, dx = \int_0^1 (\ln^2(x))/(1-x) \, dx \\\\ = \sum_(m=0)^\infty \int_0^1 x^m \ln^2(x) \, dx \\\\ = \sum_(m=0)^\infty -\frac2{m+1} \int_0^1 x^m \ln(x) \, dx \\\\ = \sum_(m=0)^\infty \frac2{(m+1)^2} \int_0^1 x^m \, dx \\\\ = 2 \sum_(m=0)^\infty \frac1{(m+1)^3} \\\\ = 2 \sum_(m=1)^\infty \frac1{m^3} = 2\zeta(3)`

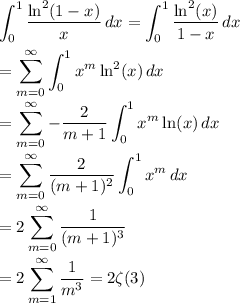
We can generalize this method to k indices to show that

`\displaystyle \sum_(n_1=1)^\infty \sum_(n_2=1)^\infty \cdots \sum_(n_k=1)^\infty \frac1{n_1n_2\cdots n_k(n_1+n_2+\cdots+n_k)} = (-1)^k \int_0^1 \frac{\ln^k(1-x)}x \, dx \\\\ = k!\,\zeta(k+1) = \Gamma(k+1)\zeta(k+1)`

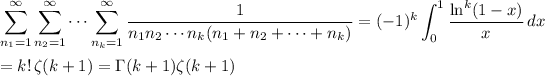
Then the sum we want is

`\displaystyle \sum_(n_1=1)^\infty \sum_(n_2=1)^\infty \cdots \sum_{n_(2022)=1}^\infty \frac1{n_1n_2\cdots n_(2022)(n_1+n_2+\cdots+n_(2022))} = \boxed{\Gamma(2023)\zeta(2023)}`