Question

(Score for Question 1:

of 5 points)
1. Suzette ran and biked for a total of 80 miles in 9 hours. Her average running speed was 5 miles per hour
(mph) and her average biking speed was 12 mph,
Let x = total hours Suzette ran.
Let y = total hours Suzette biked.
Use substitution to solve for x and y. Show your work. Check your solution.
(a) How many hours did Suzette run? I
(b) How many hours did she bike?
Answer:​

Answer 1

A) 4 Hours (of running)

B) 5 Hours (of biking)

Explanation:

So Suzette ran and biked for a total of 80 miles,

and she did all of that in 9 hours.

Let x equal the total hours of Suzette ran and let y equal the total hours of Suzette biked.

Therefore:

`x+y=9`

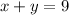
This represents the total hours. We know that the hours she had ran and biked totals 9. Thus, x plus y must equal 9.

And also:

`5x+12y=80`

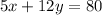
The 5x represents the miles she had ran in x hours, while the 12x represents the miles she had biked in y hours. All together, they must equal 80 miles total.

Therefore, our system is:

`x+y=9\\5x+12y=9`

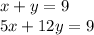
We can solve this using substitution. First, subtract x from the top equation:

`x+y=9\\y=9-x`

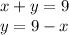
Now, substitute the y into the second equation:

`5x+12y=80\\5x+12(9-x)=80`

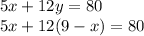
Distribute:

`5x+108-12x=80`

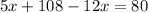
Combine like terms:

`-7x+108=80`

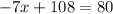
Subtract 108 from both sides:

`(-7x+108)-108=(80)-108\\-7x=-28`

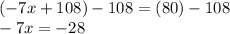
Divide both sides by -4:

`x=4`

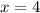
Therefore, Suzette ran for a total of 4 hours.

Since she biked and ran for a total of 9 hours, she must have biked for 9-4 or 5 hours.

Checking:

4 hours of running plus 5 hours of biking does indeed equal 9 hours total:

`4(5)+5(12)=20+60=80`

So by running 5mph for 4 hours and by biking 12mph for 5 hours, she did indeed reach a total of 80 miles.