Answer:
x=35°
Explanation:
So first, recall that the interior angles of a triangle must total 180°.
The sum of the angles for the given triangle can be described by:

Since the total must equal 180°, set the expression equal to 180°.

To find the value of x, we just need to solve for x.
To start, subtract 110 from both sides. The 110s on the left cancels:
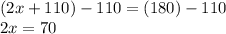
Now, divide both sides by 2. The 2s on the left cancel.
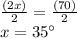
Therefore, the value of x is 35°.