Question

If the mZSRW=85 degrees what are the measures of ZVRU and ZURW?​

Answer 1

m<VRU = 80°

m<URW = 15°

Explanation:

<SRW and <VRT are vertical opposite angles. Vertical opposite angles are equal. Therefore:

`2x + 15 = 85`

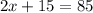
Use this expression to solve for the value of x

`2x + 15 - 15 = 85 - 15`

`2x = 70`

`(2x)/(2) = (70)/(2)`

`x = 35`

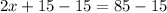
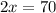
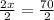
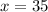
Find m<VRU by plugging in the value of x in the expression for its angle given.

m<VRU = [tex] 2x + 10 [tex]

[tex] 2(35) + 10 = 70 + 10 = 80 [tex]

m<VRU = 80°

FIND m<URW.

m<URW = 180° - (m<VRU + m<SRW) (angles on a straight line is 180°)

m<URW = 180 - (80 + 85)

= 180 - 165

m<URW = 15°