Each point is of the form (x,y). We replace x with some number to get a paired y value.
For instance, if x = 1, then,
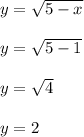
Meaning x = 1 and y = 2 pair up. The point (x,y) = (1,2) is on the curve.
Then let's try x = 4

Showing (4,1) is also on the curve.
The point (5,0) is also on the curve too because of the steps below
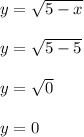
We can't go any higher than x = 5 or else the expression 5-x will be negative. Eg: if x = 7, then 5-x = 5-7 = -2. We cannot take the square root of a negative and get some real number output.
So let's go in the opposite direction. Let's try x = -4
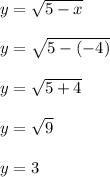
Showing (-4,3) is also on the curve.
The x values I'm picking are such that the y value is an integer. For the majority of the x values, you'll get some decimal value which is a bit tricky to graph on paper. So effectively you'll have to use trial and error to find the right x values to pick. The goal is to get the stuff under the square root to simplify to some perfect square (0,1,4,9,...etc)
After generating enough points, you draw a curve through them all. The more points, the more accurate the graph.