Question

Please help me please thank you

Answer 1

x=15

Explanation:

Angles 2 and 4 are same-side interior angles. This means that if they are supplementary angles, then the lines A and B are parallel.

Supplementary angles, when added together, will equal a total of 180°. Set up an equation in which the angles are added and are equal to 180:

`(2x+10)+(4x+80)=180`

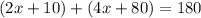
Solve for x. Remove the parentheses and combine like terms:

`2x+10+4x+80=180\\\\2x+4x+10+80=180\\\\6x+90=180`

Work to isolate the variable, x. Subtract 90 from both sides:

`6x+90-90=180-90\\\\6x=90`

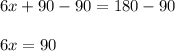
Isolate x. Divide both sides by 6:

`(6x)/(6)=(90)/(6) \\\\x=15`

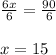
The value of x is 15.

:Done

If you want to check your work, insert the value of x into the angles, and add them. If the answer is 180, then the value of x is true:

`2x+10\\\\2(15)+10\\\\30+10\\\\40`

∠2=40

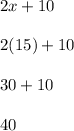
`4x+80\\\\4(15)+80\\\\60+80\\\\140`

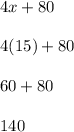
∠4=140

∠2+∠4=180

40+140=180

The value of x is true.

Answer 2

x = 15

Explanation:

angles 2 and 4 are supplementary so they add up to 180

2x + 10 + 4x + 80 = 180

6x + 90 = 180

6x = 90

x = 15