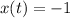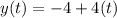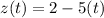Question

The vector parametric equation for the line through the points (−1,−4,2) and (−1,0,−3) is:_______

Answer 1

Answer:
`x(t)=-1`

`y(t)=-4+4(t)`

`z(t)=2-5(t)`

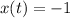
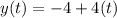
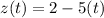
Explanation:

To find: The vector parametric equations for the line through the points (−1,−4,2) and (−1,0,−3).

Let A (−1,−4,2) and B(−1,0,−3)

First we find direction vectors :
`\overrightarrow{AB}=<-1-(-1),0-(-4),-3-2>`

`<0,4,-5>`

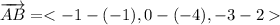
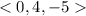
Now, the parametric equations of the line:

`x(t)=-1+0(t)`

`y(t)=-4+4(t)`

`z(t)=2-5(t)`

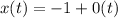
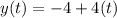
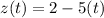
Hence, the vector parametric equations for the line through the points (−1,−4,2) and (−1,0,−3):

`x(t)=-1`

`y(t)=-4+4(t)`

`z(t)=2-5(t)`