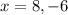Question

The following equation has how many solutions? \left|x-1\right|=7 ∣x−1∣=7

Answer 1

Two solutions.

`x = 8, -6`

Explanation:

Given the equation:

`\left|x-1\right|=7`

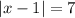
To find:

Number of solutions to the equation.

Solution:

First of all, let us learn about modulus function.

`|x|=\left \{ {{x\ if\ x>0} \atop {-x\ if\ x<0}} \right.`

i.e. Modulus function changes to positive by adding a negative sign to the negative values.

It has a value equal to
`x` when
`x` is positive.

It has a value equal to -
`x` when
`x` is negative.

Here, the function is:

`|x-1|=7`

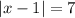
So, two values are possible for the modulus function:

`\pm(x-1)=7`

Solving one by one:

`x-1 = 7\\\Rightarrow x =8`

`-(x-1) = 7\\\Rightarrow -x+1=7\\\Rightarrow x = -6`

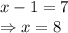
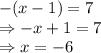
So, there are two solutions,
`x = 8, -6`