Question

Find the volume of the solid, please

Answer 1

`V \approx=1436.8`

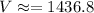
Explanation:

Variables and symbols:

• r = radius
• V = volume
• A = surface area
• C = circumference
• π = pi = 3.1415926535898
• √ = square root

Volume of a sphere in terms of radius:

`V = (4)/(3)\pi r^3` ,
`V \approx 4.1888r^3`

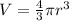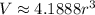
To calculate the volume of a sphere:

Usually the hardest part is measuring or estimating the diameter of the sphere. Special tools exist for smaller parts like balls in ball-bearings, but it gets more complicated if the size is large. Knowing that the diameter is the largest internal measurement you can take should help.

Once you have the measurement, to find the volume use the formula above, in which π is the well-known mathematical constant equal to about 3.14159. To adjust for a half-sphere calculation, just divide the result by two.

Spheres and half-spheres are useful in engineering and architecture due to their property of being able to take equal amounts of pressure or force from each direction.

Solution:

`V=(4)/(3) \pi r^(3) =(4)/(3) *\pi *7^(3) \approx1436.75504`

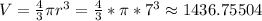
Round to nearest tenth:
`1436.8`

Answer 2

1436.8 mi (nearest tenth)

Explanation:

Volume of a sphere

`\sf V=\frac43 \pi r^3`

(where r is the radius)

Given:

• r = 7 mi

Substituting given value into the equation and solving for V:

`\begin{aligned}\implies \sf V &=\frac43 \pi (7)^3\\\\ & = (1372)/(3) \pi \\\\& = 1436.75504\\\\& =1436.8\: \sf mi \:(nearest\:tenth) \end{aligned}`