Explanation:
Since the focus is on the right in relation to the directrix, the parabola will open right.
Next, for a parabola opening to the right. the formula is
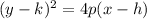
where (h,k) is the vertex.
P is the midpoint of the total distance between the focus and directrix.
Since the parabola is opening right, our vertex and focus will lie on the x axis.
The vertex lies halfway between directrix and focus so the vertex is at
(5,-5).
Note: We choose the point (3,-5) for the directrix because the focus also have (7,-5).
This means p=2.

So our vertex is (5,-5) p=2,
opens right