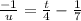Question

1. Use separation of variables to find the solution to the differential equation subject to the given initial condition.

dy/dx = 5y/x, y = 4 while x = 1
2. Find the solution to the differential equation, subject to the given initial condition.
4(du/dt) = u^2, u(0) = 7

Answer 1

Explanation:

Given the differential equation dy/dx = 5y/x subject to the condition y = 4 and x = 1. Using the variable separable method of solving differential equation, we will have;

dy/dx = 5y/x

Separate the variables

dy/5y = dx/x

Integrate both sides of the expression

`(1)/(5)\int\limits (1)/(y) \, dy = \int\limits (dx)/(x) \\ \\(1)/(5)lny = lnx + C\\\\lny = 5lnx+5C\\`

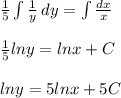
using the initial condition y = 4 while x = 1

ln4 = 5ln1 + 5C

ln4 = 0+5C

C = ln4/5

Substituting the value of C back into the expression;

`lny = 5 lnx+5(ln4/5)\\lny = 5lnx+ln4\\lny = lnx^5+ln4\\lny = ln(4x^5)\\y = 4x^5`

Hence the solution to the differential equation is y = 4x⁵

b) Given 4(du/dt) = u²

du/dt = u²/4

du/ u² = dt/4

u⁻²du = 1/4 dt

integrate both sides of the equation

`\int\limit {u^(-2)} \, du = \int\limits(1)/(4) \, dt\\\\(u^(-1))/(-1) = (t)/(4) + C\\\\(-1)/(u) = (t)/(4) + C`

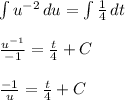
Imputing the initial condition u(0) = 7 i.e when t = 0, u = 7

`(-1)/(7) = (0)/(4) + C\\\\(-1)/(7) = C\\`

`(-1)/(u) = (t)/(4) - (1)/(7)`

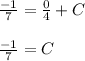
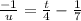
Hence the solution to the DE is
`(-1)/(u) = (t)/(4) - (1)/(7)`