Question

Solve the following equations by factorisation method.Only factorisation not dharacharya.​

Answer 1

Hello, please consider the following.

When
`x_1` and
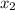`x_2` are two roots, we can factorise as

`ax^2+bx+c=a(x-x_1)(x-x_2)=a(x^2-(x_1+x_2)x+x_1x_2)=0`

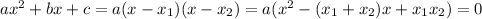
So for the first equation, we can say that the sum of the zeros is

`(a^2+b^2)/(2)=(a^2)/(2)+(b^2)/(2)`

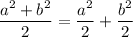
and the product is

`(a^2b^2)/(4)=(a^2)/(2)(b^2)/(2)`

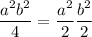
So we can factorise as below.

`4x^2-2(a^2+b^2)x+a^2b^2=(2x-a^2)(2x-b^2)=0`

And the solutions are

`\boxed{\sf \\\bf \ (a^2)/(2) \ \ and \ \ (b^2)/(2)}`

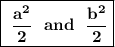
For the second equation, we will complete the square and put the constant on the right side and take the root.

Let's do it!

`9x^2-9(a+b)x+2a^2+5ab+2b^2=0\\\\9(x-(a+b)/(2))^2-9((a+b)^2)/(4)+2a^2+5ab+2b^2=0\\\\9(x-(a+b)/(2))^2=(9(a+b)^2-8a^2-20ab-8b^2)/(4)\\\\9(x-(a+b)/(2))^2=(9a^2+18ab+9b^2-8a^2-20ab-8b^2)/(4)\\\\9(x-(a+b)/(2))^2=(a^2+b^2-2ab)/(4)=((a-b)^2)/(4)\\\\(x-(a+b)/(2))^2=((a-b)^2)/(2^2\cdot 3^2)`

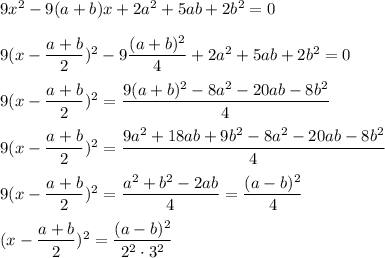
We take the root, and we find the two solutions

`\begin{aligned}x_1&=(a+b)/(2)-(a-b)/(6)\\\\&=(3a+3b-a+b)/(6)\\\\&=(2a+4b)/(6)\\\\&\boxed{=(a+2b)/(3)}\end{aligned}`

`\begin{aligned}x_1&=(a+b)/(2)+(a-b)/(6)\\\\&=(3a+3b+a-b)/(6)\\\\&=(4a+2b)/(6)\\\\&\boxed{=(2a+b)/(3)}\end{aligned}`

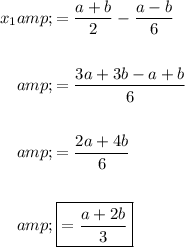
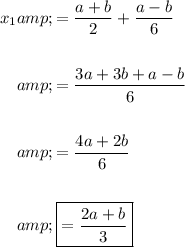
Thank you.