Question

Please help ASAP PLEASE

Jane is trying to decide between two savings account plans. Plan A offers a
quarterly compounded interest rate of 0.15%, while Plan B offers 0.5% interest
compounded annually. Which is the better plan? By how much?

Answer 1

The answer is below

Explanation:

The compound interest is given by the formula:

`A=P(1+(r)/(n) )^(nt)\\\\Where\ A \ is\ the\ final \ amount, P\ is\ the \ principal\ or \ initial\ amount,r\ is\ the\ rate\\n\ is\ the\ number\ of \ times\ compounded\ per\ period\ and \ t\ is\ the\ number\ of\ periods.\\`

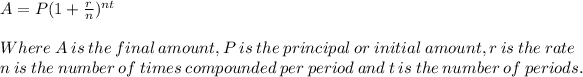
For the same amount of principal (P) for both plan A and B:

Plan A offers a quarterly compounded interest rate of 0.15%. That is r = 0.15% = 0.0015, n = 4. Therefore:

`A_a=P(1+(0.0015)/(4) )^(4t)\\\\A_a=P(1+0.000375)^(4t)\\\\A_a=P(1.000375)^(4t)`

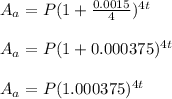
Plan B offers annual compounded interest rate of 0.5%. That is r = 0.5% = 0.005, n = 1. Therefore:

`A_b=P(1+(0.005)/(1) )^(t)\\\\A_b=P(1.005)^(t)\\\\The\ ratio\ of\ their\ interest:\\\\(A_a)/(A_b) =(P(1.000375)^(4t))/(P(1.005)^(t)) \\\\(A_a)/(A_b) =((1.000375)^(4t))/((1.005)^(t)) \\\\For\ the\ same\ time\ period\ of\ one\ year(t)=1\\\\(A_a)/(A_b) =((1.000375)^(4(1)))/((1.005)^(1)) \\\\(A_a)/(A_b) =(1.0015)/(1.005) \\\\A_b=(1.005A_a)/(1.0015)\\ \\A_b=1.003A_b`

Plan B is the better plan, it is greater by a factor of 1.003