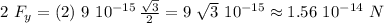Question

Three identical point charges, Q = 2 PC, are placed at the vertices of an equilateral triangle as shown in the figure. The length of each side of the triangle is d

= 2 m. Determine the magnitude and direction of the total electrostatic force on the charge at the top of the triangle.

Answer 1

The total force on the charge at the top of the triangle is approximately

`1.56\,\,10^(-14)\,\,N`

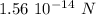
Step-by-step explanation:

Please look at the attached image to follow the explanation.

Since all charges are of the same positive value, the force exerted on the top charge by the other two are going to be on the line that joins the top charge with each of the other vertices of the triangle, pointing away from the top charge (illustrated by green vectors of the same length in the image).

We need to find the x and y components of these force vectors in order to find the resultant force by combining the x components among themselves, and the y components among themselves. Notice that the angle needed is in all cases
`60^o`.

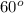The x- components include the cosine of
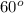`60^o`, while the y components include the sine of
`60^o`.

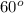Notice as well that the x-components cancel each other (they have the same magnitude but point in opposite directions), while the y-components are both of the same value but pointing in the same direction (pointing up).

Then we just need to multiply by two the y component of one of the forces to find this total force.

Now, the magnitude of the forces in question are given by Coulomb's Law:

`F_C=k\,(q_1\,\,q_2)/(d^2) =9\,\,10^9\,(2\,\,10^(-12)\,\,2\,\,10^(-12))/(2^2) =9\,\,10^(-15)\,\,N`

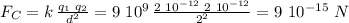
therefore we can calculate what the y-component of this is using:

`F_y=F\,sin(60^o)=9\,\,10^(-15) \,(√(3) )/(2) \\`

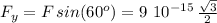
and twice this value becomes:

`2\, \,F_y=(2)\,\,9\,\,10^(-15) \,(√(3) )/(2)=9\,\,√(3) \,\,10^(-15)\approx 1.56\,\,10^(-14)\,\,N`