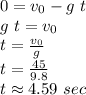Answer:
The time to reach the maximum height is approximately 4.59 seconds
Step-by-step explanation:
The maximum height in a problem where friction with the air is neglected, only needs the kinematic information of the initial velocity at which the object was launched vertically.
Recall that the formula for the velocity of an object under constant acceleration (
 ) in terms of time (t) is given by:
) in terms of time (t) is given by:
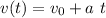
where
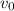 is the initial velocity of the object (in our case the speed at which it was launched up in the air = 45 m/s)
is the initial velocity of the object (in our case the speed at which it was launched up in the air = 45 m/s)
Considering that the acceleration the object is subjected (which is the acceleration of gravity g = 9.8 m/s^2) is acting in opposite direction to the initial velocity of the object, we make sure to include a negative sign in the formula:
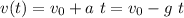
then, considering that at the time the object reaches its maximum height, is when it stops and starts it motion back towards earth, that is the point at which the object's velocity is zero. Then we can solve for the time as follos: