Question

Prove the cofunction Identity using the Addition and Subtraction Formulas. Tan (pi/2 - u) = cot (u) Since tan (pi/2) is undefined, use a Reciprocal Identity, and then use the Substitution Formulas to simplify. Tan (pi/2 - u) = sin/cos (pi/2 - u) = (cos (u)) - (cos (pi/2)) (sin (u))/(sod (pi/2)) (cos (u)) + (sin (pi/2)) (sin (u)) = (cos (u)) - (0) (sin (u))/(0) (cos (u)) + (1) (sin (u)) =/sin (u)

Answer 1

Explanation:

We are to prove the cofunction Identity using the Addition and Subtraction Formulas.
`tan(\pi/2 - u) = cot (u)`

From trigonometry identity,
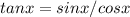`tan x = sinx/cosx`, starting from right hand side of the equation, the expression above will become;

`tan(\pi/2 - u) = (sin((\pi)/(2)-u ))/(cos((\pi)/(2)-u) )........ \ 1 \\\\from\ quadrant;\\\\sin((\pi)/(2)-u) = cos (u) \ and \ cos((\pi)/(2)-u) = sin(u)`

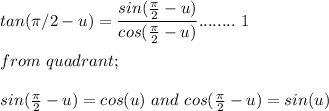
Substituting this trigonometry identities into equation 1 we will have;

`tan(\pi/2 - u) = (cos(u))/(sin(u))`

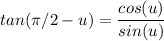
Since cot(u) = 1/tan(u) = cos(u)/sin(u), hence;

`tan(\pi/2 - u) = (cos(u))/(sin(u)) = cot(u)\\\\tan(\pi/2 - u) = cot (u)\ Proved!`