Question

What is the product of complex conjugates? The product of complex conjugates is a difference of two squares and is always a real number. The product of complex conjugates is the same as the product of opposites. The product of complex conjugates may be written in standard form as a+bi where neither a nor b is zero. The product of complex conjugates is a sum of two squares and is always a real number.

Answer 1

(a + bi)(a – bi) = a2 – (bi)2 = a2 + b2

The product of a complex number and its complex conjugate is

✔ always

a real number.

Answer 2

Last given option is the correct answer:

"The product of complex conjugates is a sum of two squares and is always a real number."

Explanation:

The product of two conjugates can be described and solved like this:

`(a + b\,i) \,(a - b\,i)= a^2-a\,b\.i+a\,b\,i-b^2\,i^2=a^2+0-b^2\,(-1)= a^2+b^2`

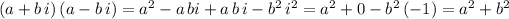
so, no matter what the values for the real values a and b are, the product is always a real number and the sum of two squares.