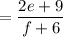Question

`({4e }^(2) + 16e - 9) / (2ef + 12e - f - 6)`
please help me solve this problem​

Answer 1

Step-by-step explanation

`(4e^2+16e-9)/(2ef+12e-f-6)`

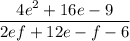
⇒ First, factor the numerator by grouping:

`=(4e^2-2e+18e-9)/(2ef+12e-f-6)\\\\\\=(2e(2e-1)+9(2e-1))/(2ef+12e-f-6)\\\\\\=((2e+9)(2e-1))/(2ef+12e-f-6)`

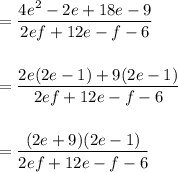
⇒ Now, factor the denominator by grouping:

`=((2e+9)(2e-1))/(2e(f+6)-(f+6))\\\\\\=((2e+9)(2e-1))/((2e-1)(f+6))`

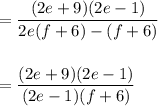
⇒ We must determine which values of e and f are unacceptable, meaning, will make this expression undefined. These will be the values of e and f that make the denominator equal to 0.

• ⇒ To find these values, let's set each term in the denominator equal to 0, and solve for e and f.
• 
  `2e-1=0` ⇒
  `2e=1` ⇒
  `e=(1)/(2)`
• 
  `f+6=0` ⇒
  `f=-6`
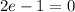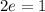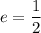
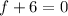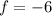
• ⇒ The restrictions for e and f include
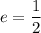  `e=(1)/(2)` and
  `f=-6`.

`=((2e+9)(2e-1))/((2e-1)(f+6))`

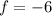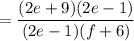
⇒ Reduce values in the numerator and denominator:

`=((2e+9))/((f+6))\\\\\\=(2e+9)/(f+6)`

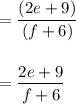
Answer

`=(2e+9)/(f+6)`