Question

A number has the property that its square is equal to 84 more than five times the number. Enter all numbers that have this property.

Answer 1

The numbers for which the given property hold true are 12 and -7

Explanation:

Let the number be
`x`.

As per the given statement:

Square of the number (
`x^(2)`) is 84 more than five times of the number (
`5x+84`).

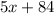Writing in the equation form:

`x^(2) =5x+84`

To find:

All the numbers for which above equation holds true.

Solution:

`x^(2) =5x+84`

Let us solve the above equation by rearranging the terms and then let us find the roots of the equation.

It is a quadratic equation(i.e. maximum power of
`x` is 2) so it will have 2 solutions i.e. 2 values of
`x` for which the above equation will hold true.

`x^(2) -5x-84=0`

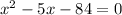
Let us factorize the equation.

`\Rightarrow x^(2) -12x+7x-84=0\\\Rightarrow x(x -12)+7(x-12)=0\\\Rightarrow (x+7)(x-12)=0\\\Rightarrow \bold{x=12, -7 }`

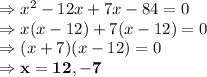
So, the numbers for which the given property hold true are 12 and -7.