Mean:
The mean of the data is the average number of the data. The average (mean) can be determined by adding all the numbers in the data and dividing it by the total digits in the data.
Given data:
- 39, 31, 28, 26, 63, 38, 28, 4, and 92
We know:
- Added data: 39 + 31 + 28 + 26 + 63 + 38 + 28 + 4 + 92
- Total digits in data: 9
Therefore, the expression that represents the mean is;
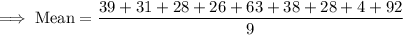
When simplified, we get;

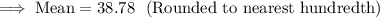
Therefore, the mean is 38.78 (Nearest hundredth).
Median:
The median can be determined by arranging the data in ascending form or descending form. Then, simply determine the middle number. The middle number of the data (in ascending or descending order) is the median.
Data (In ascending order):
4, 26, 28, 28, 31, 38, 39, 63, 92
As the number of digits is odd, we will use the rule [(n + 1)/2], where "n" is the number of digits in the data.
Total digits in data: 9
- ⇒ (n + 1)/2 th
- ⇒ (9 + 1)/2 th
- ⇒ (10)/2 th
- ⇒ 5th
The 5th digit in the "ascending order" data is the median.
- ⇒ 4, 26, 28, 28, 31, 38, 39, 63, 92
The median of the data is 31.
Mode:
The mode of the data is the digit that has repeated the most. We can determine the mode of the data by preparing a frequency table.

Looking at the table, we can see that 28 has repeated 2 times and has repeated the most. Therefore, 28 is the mode.