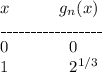Question

A company ships coffee mugs using boxes in the shape of cubes. The function g(x) = gives the side length, in inches, for a cube with a volume of x cubic inches. Suppose the company decides to double the volume of the box. Which graph represents the new function?

Answer 1

c

Explanation:

Answer 2

The graph is attached below.

Explanation:

The volume of the box containing the coffee mugs is,

`V=x^(3)`

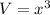
Then the function representing the side length, in inches, for the box is:

`g(x)=x`

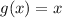
Now, it is provided that the company decides to double the volume of the box.

That is, the new volume will be:

`V_(n)=2x^(3)`

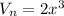
Then the side length, in inches, for the box will be:

`g_(n)(x)=\sqrt[3]{2x^(3)} =\sqrt[3]{2}x`

Then the graph representing the function, formed using the following points is:

`x\ \ \ \ \ \ \ \ \ g_(n)(x)\\\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\0\ \ \ \ \ \ \ \ \ \ \ 0\\1\ \ \ \ \ \ \ \ \ \ \ 2^(1/3)`